今回は、「逆三角関数」についての説明です。
1.逆三角関数とは?
アークサイン・アークコサイン・アークタンジェントって聞いたことありませんか?
sin-1α・cos-1α・tan-1αという書き方が一般的です。
arcsin・arccos・arctanと書くこともあるようです。
sin-1x=(sinx)-1なので、それぞれsin-1α=1/sinα、cos-1α=1/cosα、tan-1α=1/tanαに該当します。
三角関数の二乗の関係がよくわからない場合は先に以下の記事を読んでみた方がいいかもです。
1/sinα、1/cosα、1/tanαという形からわかる通り、各々がsinα・cosα・tanαの逆関数を指しています。
逆関数がわからない人向けに補足しますが、逆関数とは縦軸y横軸xのグラフにて、y=xを基準として対称になる関数のことです。
例えば、図1のy=2xとy=x/2の2式は逆関数の関係にあります。
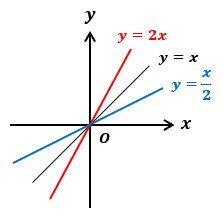
ある関数の逆関数は、ある関数においてyとxを入れ替えたものになります。
y=2xという関数の場合、yとxを入れ替えるとx=2y。
移項するとy=x/2になり、これが逆関数になっているわけです。
アークサイン・アークコサイン・アークタンジェントの逆三角関数は、直角三角形の角度を求める際に使用します。
具体的に言うと、「直角三角形にて、ある角度の時の二つの辺の長さの比を表したもの」が三角関数でしたので、それとは逆に「直角三角形にて、二つの辺の長さの比がわかっている時の角度を表したもの」が逆三角関数です。
求めるものが逆転しているわけですね。
ちなみに、”アーク”である理由は、逆三角関数がアーク(arc=円弧)の長さを返す関数になることが由来になっているらしいです。
2.逆関数の範囲
y=xを基準として対称になる関数が逆関数でしたので、y=sinxとその逆関数のy=sin-1xを図示すると以下のようになります。
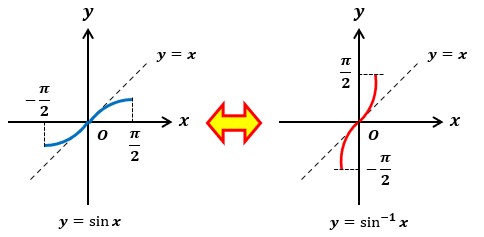
y=sinxは-π/2≦x≦π/2の範囲しか描かれていませんね。
こうなっている理由は、yの値が定まったらxの値も定まるという一対一の関係であることが逆関数が存在する為の条件だからです。
具体的に言うと、y=sin(π/6)=1/2とy=sin(5π/6)=/1/2の関係のように、y=1/2の時のxがπ/6と5π/6の複数パターンあるような関数に対しては逆関数が存在しないということです。
ですが、y=sinxの場合は-π/2≦x≦π/2の範囲内においてはyとxに一対一の関係が成り立っているので、その範囲内でなら逆関数が存在することになります。
このように、逆三角関数は範囲に注意が必要になります。
ちなみに、y=cosxの場合は0≦x≦π、y=tanxの場合は-π/2<x<π/2と微妙に範囲が異なります。
以上、「逆三角関数」についての説明でした。
【基礎から学ぶ三角関数】
◎三角関数の基礎 ~sin・cos・tanとはそもそも何?
◎三角関数と正弦曲線の関係 ~sin波とcos波について
◎sinθの2乗 ~2の付く位置について
◎三角関数と象限 ~角度と符号の関係
◎正弦定理 ~三角形の辺と対角の関係
◎余弦定理 ~三角形の角と各辺の関係
◎加法定理とは? ~sin(α+β)の解法
◎積和の公式 ~sinαcosβなどの解法
◎和積の公式 ~sinα+sinβなどの解法
◎二倍角の公式 ~sin2αなどの解法
◎半角の公式 ~sin(α/2)の2乗などの解法
◎逆三角関数 ~アークサインやアークコサインとは?

