今回は、「n進法」についての説明です。
1.初めに
数字の表し方は色々あります。
私達が普段日常生活で使用している0~9の10種類の数字で表す方法は10進法と言います。
普通に過ごす分にはこれだけ知っていれば何も困らないのですが、社会に出ると業種によってはそうもいきません。
当たり前のように2進法や16進法といったものが出現します。
この記事では、そんな数字の表し方について説明していきます。
難しい言い回しはなるべく回避して、初見の方でも(多分)理解できるようにまとめたつもりです。
2.n進法とは?
数字の表し方は、2進法・8進法・10進法・16進法などがあります。
それぞれの表し方は、以下のルールに則っています。
2進法:0~1の2種類の数字で表す。
8進法:0~7の8種類の数字で表す。
10進法:0~9の10種類の数字で表す。
16進法:0~9の10種類の数字とA~Fの6種類のアルファベットの計16種類で表す。
見てわかると思いますが、取り扱う文字の数と進法の前の数字部分が一致していますね。
この数のことを基数と呼びます。
つまり、n進法(nには数字が入る)とは基数がnの表し方を指しているということです。
さて、0~1で表す、0~7で表すと言われてもピンとこないと思いますので実際の例を見てみましょう。
普段使用している「10」という数字を2進法・8進法・10進法・16進法で表すと、以下のようになります。
2進法:1010
8進法:12
10進法:10
16進法:0A
現時点では意味不明だと思いますが、この記事を読み終える頃には普通に理解できるようになっていると思います。(願望)
3.10進法について
まずは、馴染みの深い10進法について考えてみましょう。
10進法は0~9の数字で表されます。
0~9しか使えないので、「09」から1増やすと9が0になり、桁が上がって0が1になることで「10」という並びになります。
ここで増えた1という数字は「10が1つある」ことを示しています。
同様に、100という数字の「1」は「100が1つある」ことを指しているわけですが、これは言い方を変えると「10の二乗が1つある」と言えます。
はい、乗数の登場です。
乗数とは、2×2のような同じ数字同士の掛け算を22といった形式で表示したものです。
2の三乗(2×2×2)なら23になります。
ここでは『そうやって表されるんだ』程度の理解で充分です。
結局のところ何が言いたいかというと、10進法は以下のようなルールに従って表示されているということです。
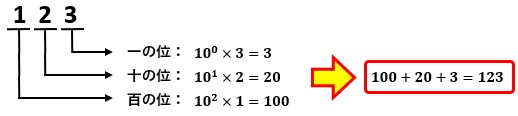
つまり、10進数で3桁の数字があった場合、厳密には一番右の数字に100を掛けた値と右から二番目の数字に101を掛けた値と右から三番目の数字に102を掛けた値の総和になっているのです。
(ちなみに、何かの0乗(10,50,100など)は1固定です。)
10進法は慣れ親しんだものなので、わざわざこんな考え方をしなくても理解できると思いますが、他のn進法を理解する上でこの考え方が重要になるのでちゃんと理解しましょう。
というか、この考え方さえわかっていれば他のn進法も自ずと理解できます。
4.2,4,8進法について
では、2進法の説明に移ります。
2進法は0~1の数字で表されます。
0~1しか使えないので、「01」から1増やすと1が0になり、桁が上がって0が1になることで「10」という並びになります。
ここで増えた1という数字は「2が1つある」ことを示しています。
つまり、10進数でいうところの「2」は、2進数では「10」と表示するわけです。
読み方は”いちぜろ”か”いちまる”が多く、少なくとも”じゅう”ではないです。
この時点で気付くと思うのですが、基数が変わっただけで考え方は10進法と全く同じです。
試しに2進数を10進数で表してみると以下のようになります。

どうですか?ルールさえ覚えてしまえば簡単でしょう?
“1”増えると一番右に”1″が足されていく、0と1で表現できなくなったら桁が上がる、これだけです。
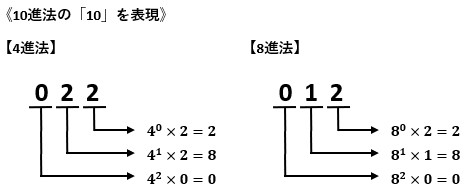
4進法と8進法も考え方は同じです。
4進法は0~3、8進法は0~7で表現されるようになるだけです。
使うことはないだろうと思いますが、練習にはなりますし、一応例を載せておきますね。
2進法は、コンピュータと密接な関係があります。
コンピュータのデータは「0」と「1」で表現され、最小単位はbitと呼ばれています。
1bitで表せるのは「0」か「1」のみです。
数値のデータは2進数でそのまま表現できますし、特定の羅列が何を意味をするか定義しておけば意味は伝わるので、コンピュータではこのbitのやり取りが高速で行われています。
特定の羅列に意味を持たすというのは、例えば「00」で「おはよう」、「01」で「こんにちは」、「10」で「こんばんは」、「11」で「おやすみ」といった具合です。
こうすれば2bitで簡単な挨拶ができますよね?
こんな仕組みなので、100bitのデータがあったら、それは100個の「0」と「1」の羅列で表現されているデータということになります。
この辺りの詳しい話は別途まとめておこうと思います。
5.16進法について
残りは問題の16進法についてです。
16進法は0~9の数字とA~Fのアルファベットで表されます。
0~9はそのまま表し、アルファベットはそれぞれ10進数の「10(A)」、「11(B)」、「12(C)」、「13(D)」、「14(E)」、「15(F)」に該当します。
A~Fも数字として扱うのが16進法ということです。
F以降のアルファベットは使えないので、「0F」から1増やすとFが0になり、桁が上がって0が1になることで「10」という並びになります。
ここで増えた1という数字は「16が1つある」ことを示しています。
つまり、10進数でいうところの「16」は、16進数では「10」と表示するわけです。
相変わらず考え方は2進法や10進法と同じなのですが、「A~Fが10~16に値する」という感覚は実際に使って慣れないことには身に付きません。
これに関しては回数をこなす他ないです。
練習として、以下の16進数を10進数で表してみましょう。
①0B 、②1C 、③20
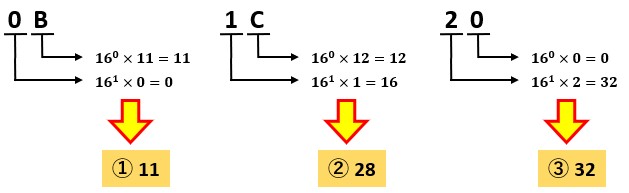
16進数は10進数と見分けがつかない場合がありますので、勘違いしないように注意してください。
…まあ、実務に関係してこない限り勘違いも何もないですけどね。
6.2進数の変換
各進法については理解できたと思いますので、最後に2進数の変換について考えていきます。
ちなみに、2進数はBinary、10進数はDecimal、16進数はHexdecimalと言います。
そして、10進数を2進数で表すことを二進化十進数(BCD:Binary-Coded Decimal)と呼んだりします。
意識高い系の方だと相手が理解しているしていないに関わらず専門用語を使いたがる為、バイナリ・デシマル・ヘキサという呼称を使用してくることがあるので注意(?)しましょう。
相手の性格によっては知らないふりして教えを乞うと評価が上がったりしますよ(笑)
さて、変換についてですが、2進数から10進数への変換はここで説明した通り普通に読み解くしかありません。
ですが、2進数から4進数・8進数・16進数は比較的容易に変換が可能です。
2進数の「1111」があるとします。
下図の橙部分に注目して欲しいのですが、橙部分のブロック単位で考えると左から0~3、0~7、0~15の範囲で表されることがわかります。
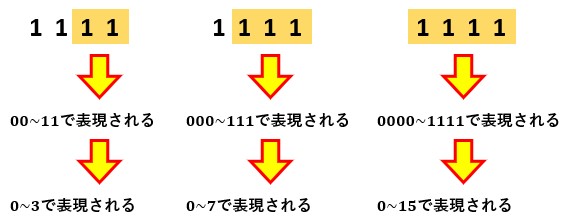
0~3、0~7、0~15という範囲、どこかで見覚えはありませんか?
それはコイツらです↓↓
4進数:0~3の数字で表現
8進数:0~7の数字で表現
16進数:0~9の数字とA~Fのアルファベットで表現⇒10進数だと0~15の数字で表現
つまり、4進数は2進数の2ブロック相当、8進数は2進数の3ブロック相当、16進数は2進数の4ブロック相当だと考えてしまえばいいわけです。
言葉ではわかりづらいので、実例を以て説明します。
2進数の「1111」を4進数・8進数・16進数に変換してみましょう。
※ 2進数の「1111」は10進数では「15」です。
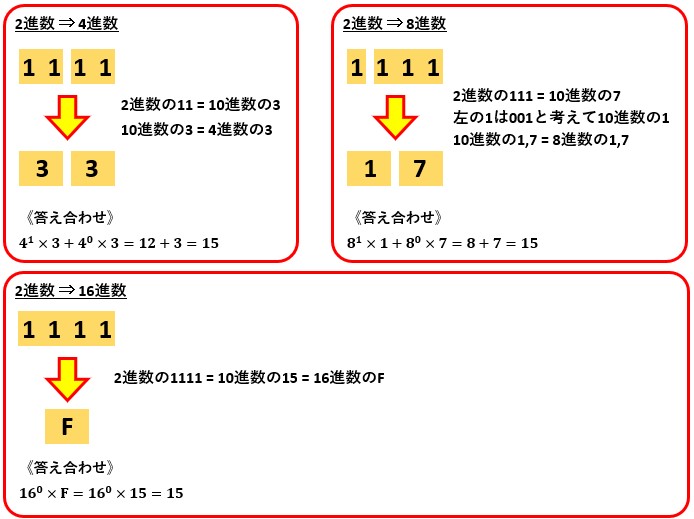
2進数が「111111111111」のように増えても上記の関係は変わらない為、覚えておくと便利です。
以上、「n進法」についての説明でした。
